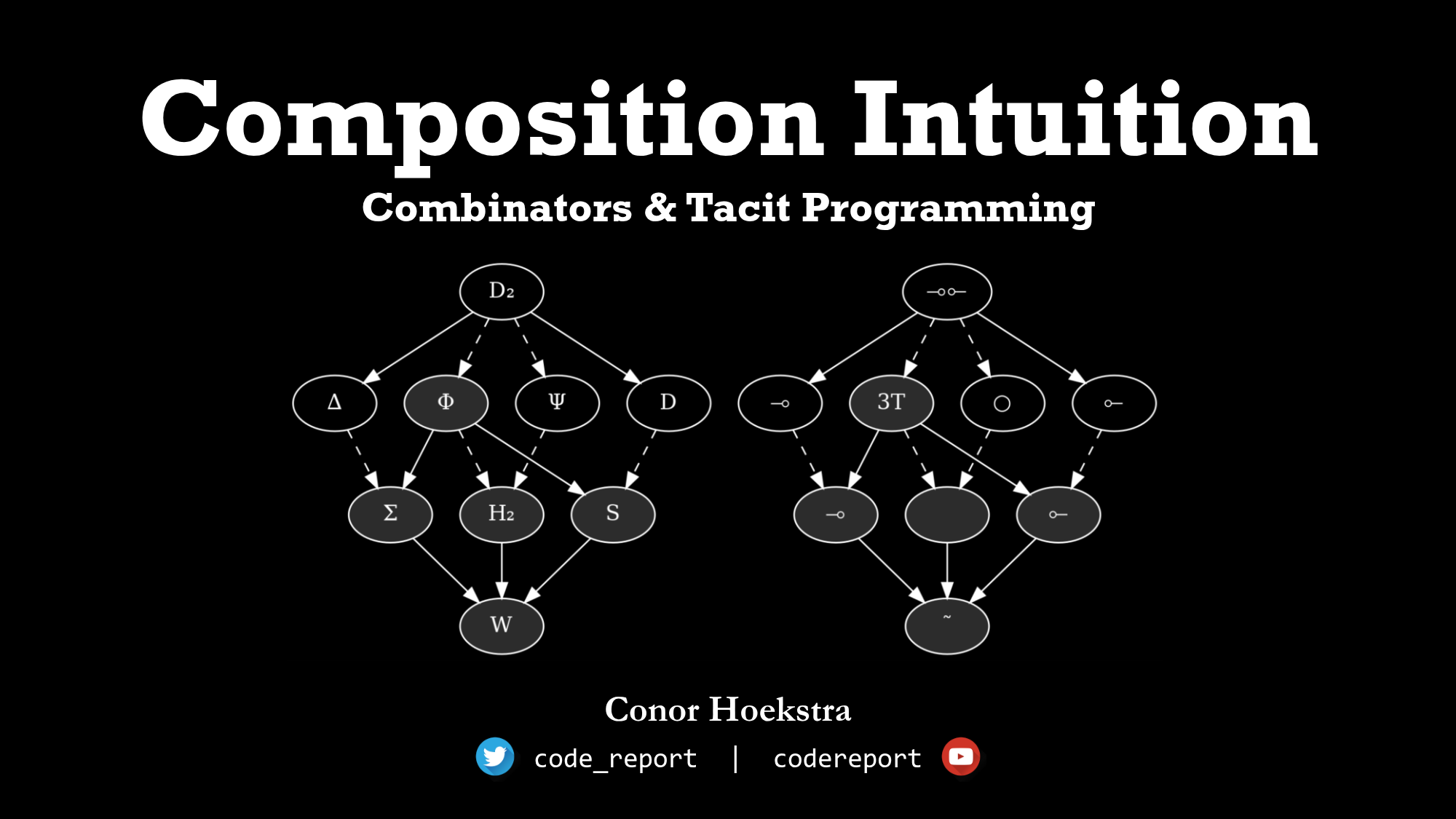
Combinatory Logic

Combinatory logic is "a theory for the foundation of mathematics... its goal was ... to establish fundamental mathematical concepts on simpler and cleaner principles than the existing mathematical frameworks... Its 'lack of (bound) variables' relates combinatory logic to the pointfree style of programming." — HaskellWiki¹

The best programming languages for programming with combinators are array languages like BQN, J and APL. Ken Iverson first introduced the S and Φ combinators as the "hook" and "fork" in the J language in the early 1990s. Dyalog APL would then later add combinators in Dyalog 14.0 in 2014. Newer array languages like BQN have the strongest support for combinator programming. More details of combinators as they exist in array languages can be found here.

If you are interested in learning more, a great starting point are the talks below.